数学有关模块

random 模块

random模块实现了各种分布的伪随机数生成器

>>> import random
#随机小数
>>> random.random()      # 大于0且小于1之间的小数
0.7664338663654585
>>> random.uniform(1,3) #大于1小于3的小数
1.6270147180533838

#随机整数
>>> random.randint(1,5)  # 大于等于1且小于等于5之间的整数 左闭右闭
>>> random.randrange(1,10,2) # 大于等于1且小于10之间的奇数 左闭右开

#随机选择一个返回
>>> random.choice([1,'23',[4,5]])  # #1或者23或者[4,5]
#随机选择多个返回，返回的个数为函数的第二个参数
>>> random.sample([1,'23',[4,5]],2) # #列表元素任意2个组合
[[4, 5], '23']

#打乱列表顺序
>>> item=[1,3,5,7,9]
>>> random.shuffle(item) # 打乱次序
>>> item
[5, 1, 3, 7, 9]
>>> random.shuffle(item)
>>> item
[5, 9, 7, 1, 3]

decimal 模块

decimal模块提供十进制数据类型，并能界定精度，由数字的字面量精准生成。

计算

>>> 0.1 + 0.2
0.30000000000000004
>>> from decimal import *
>>> Decimal('0.1') + Decimal('0.2')
Decimal('0.3')

运算符%

和普通浮点运算略有区别，Decimal 对象是取余运算而不是取模运算

使用数字字面量可以精准生成，也可以从数字生成，并来回转换

>>> Decimal(0.3)
Decimal('0.299999999999999988897769753748434595763683319091796875')
>>> Decimal.from_float(0.3) #低版本python用
Decimal('0.299999999999999988897769753748434595763683319091796875')
>>> str(Decimal(0.3))
'0.299999999999999988897769753748434595763683319091796875'
>>> float(Decimal(0.3))
0.3

其他运算方法：

• .sqrt() 平方根
• .exp() 指数
• .ln() 自然对数
• .log10() 10 为底的对数

精度界定

getcontext().prec设置有效数字，默认有效数字为 28 位

>>> getcontext().prec = 6
>>> Decimal(1) / Decimal(7)
Decimal('0.142857')

getcontext().rounding设置取舍方式，包括：

• ROUND_CEILING 向 Infinity 取舍
• ROUND_DOWN 向 0 取舍
• ROUND_FLOOR 向-Infinity 取舍
• ROUND_HALF_DOWN 半时向 0 取舍
• ROUND_HALF_EVEN 五舍六入 相当于内置函数round()
• ROUND_HALF_UP 半时向 0 反方向取舍
• ROUND_UP 向 0 反方向取舍
• ROUND_05UP 界定后是 05 则是 10 否则是 00

.quantize()舍入为固定指数

>>> Decimal('7.325').quantize(Decimal('.01'), rounding=ROUND_DOWN)
Decimal('7.32')
>>> Decimal('7.325').quantize(Decimal('1.'), rounding=ROUND_UP)
Decimal('8')

math 模块和 cmath 模块

math模块提供了对 C 标准定义的数学函数的访问，不适用于复数。

如果想得到复数结果请使用cmath模块的同名方法

常用数学常数

• pi 圆周率
• e 自然对数底数

常用数学函数

• gcd(a, b) 最大公约数
• factorial(x) 阶乘
• sqrt(x) 开平方
• log(x[, base]) 对数
• pow(x, y) 指数
• cos(x) 三角
• asin(x) 反三角
• degrees(x) radians(x) 角度弧度转化
• ceil(x) floor(x) 上下取整

statistics 模块

statistics模块用于数理统计，它主要提供了一个正态分布类 NormalDist

常用统计函数

• mean() fmean() 算术平均数 浮点数的算数平均数
• median() median_low() median_high() 中位数 低中位 高中位数
• geometric_mean() harmonic_mean() 几何平均数 调和平均数
• stdev() variance() 标准差 方差

NumPy 模块

第三方模块NumPy是使用 Python 进行科学计算的基础包。除了数学函数，随机数它包含如下的内容：

• 一个强大的 N 维数组对象.ndarray
• 复杂的（广播）功能.ufunc
• 用于集成 C / C ++和 Fortran 代码的工具
• 有用的线性代数.linalg，傅里叶变换.fft

除了明显的科学用途外，NumPy 还可以用作通用数据的高效多维容器。可以定义任意数据类型。这使 NumPy 能够无缝快速地与各种数据库集成。

一般数组

import numpy as np

a = np.arange(1, 5)  # 同np.array([1, 2, 3, 4])
a
# array([1, 2, 3, 4])

a1 = a.reshape(2, 2)  # 升维/变形
a1
# array([[1, 2],
#        [3, 4]])
np.ravel(a1)  # 降维/扁平化
# array([1, 2, 3, 4])

一般二维矩阵

和二维数组几乎无区别，只是调用方法比较便捷。

import numpy as np

a = np.mat("1 2;3 4")  # 同np.mat([[1, 2],[3, 4]])
a
# matrix([[1, 2],
#         [3, 4]])
a.I  # 逆矩阵 # 数组需要np.linalg.inv(a1)
# matrix([[-2. ,  1. ],
#         [ 1.5, -0.5]])
a.T  # 转置
# matrix([[1, 3],
#         [2, 4]])
np.asarray(a)  # 转为二维数组 #反向转换np.asmatrix(a)
# array([[1, 2],
#        [3, 4]])

绘制上帝指纹

import numpy as np
import matplotlib.pyplot as plt


def mandelbrot(w, h=None, maxit=20):
    """Returns an image of the Mandelbrot fractal of size (h,w)."""
    if h is None:
        h = w
    y, x = np.ogrid[
        -3 / 2 : 3 / 2 : h * 1j, -9 / 4 : 3 / 4 : w * 1j
    ]  # 界定的复平面坐标系的横纵轴
    c = x + y * 1j  # 界定的复平面坐标系矩阵
    divtime = maxit + np.zeros(c.shape, dtype=int)  # 初始化的权重矩阵 = 轮数+零矩阵
    z = c  # 初始化的用于迭代的复平面坐标系矩阵z
    for i in range(maxit):
        z = z**2 + c  # mandelbrot集合迭代公式
        diverge = z * np.conj(z) > 2**2  # 计算本轮发散的布尔索引
        div_now = diverge & (divtime == maxit)  # 计算比上轮新增的布尔索引
        divtime[div_now] = i  # 为新增的发散设置权重
        z[diverge] = 2  # 为发散点的值赋值 简化后续运算
        """
            这个值要大于根号2 如果不赋值 后续循环中将会溢出
            RuntimeWarning: overflow encountered in multiply
        """
    return divtime


w = int(input("输入像素值"))
plt.imshow(mandelbrot(w))

ax = plt.gca()
ax.grid(True, linestyle="-.")
plt.yticks(np.mgrid[0:w:9j], np.mgrid[3 / 2 : -3 / 2 : 9j])
plt.xticks(np.mgrid[0:w:9j], np.mgrid[-9 / 4 : 3 / 4 : 9j])
ax.spines["bottom"].set_position(("data", 1 / 2 * w))
ax.spines["left"].set_position(("data", 3 / 4 * w))
ax.spines["bottom"].set_color("white")
ax.spines["left"].set_color("white")
plt.tick_params(axis="x", colors="white")
plt.tick_params(axis="y", colors="white")
plt.savefig(
    "./mandelbrot.png",
    format="png",
    transparent=True,
    dpi=300,
    pad_inches=0,
    bbox_inches="tight",
)
plt.show()

效果图

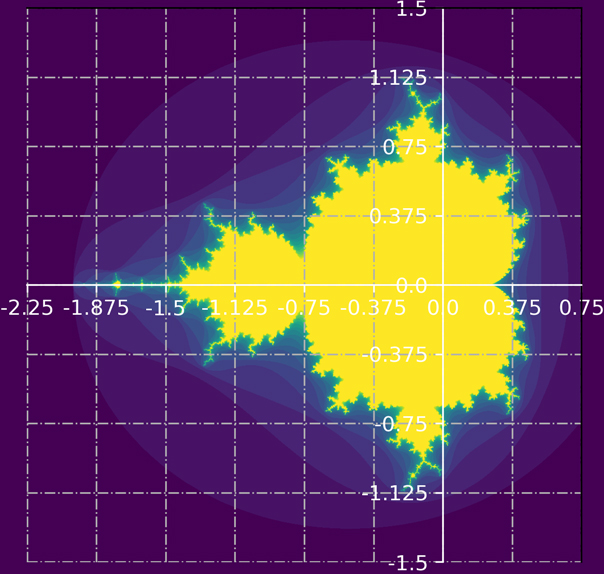
SymPy 模块

由 Python 语言编写的符号计算库。

处理数学对象的计算称为符号计算。在符号计算中，数学对象是精确表示的，而不是近似的，未计算的数学表达式会以符号形式保留

求 $$\begin{gathered} int\mathrm{\_}{0}^{+ \\ infty}{e}^{x}dx \end{gathered}$$ （oo表示 ∞）

from sympy import *

x = symbols("x")
print(integrate(exp(-x), (x, 0, oo)))

求 $$\begin{gathered} lim\mathrm{\_}x \\ to{0}^{+} \\ frac1x \end{gathered}$$

print(limit(1 / x, x, 0, "+"))